matemática divertida

Las fracciones:

es la expresión de una cantidad dividida entre otra cantidad ; es decir que representa un cociente no efectuado de números. Por razones históricas también se les llama fracción común, fracción vulgar o fracción decimal. El conjunto matemático que contiene a las fracciones es el conjunto de los números racionales

Historia:

En el Antiguo Egipto se calculaba utilizando fracciones cuyos denominadores son enteros positivos; son las primeras fracciones utilizadas para representar las partes de un entero, por medio del concepto de recíproco de un número entero.5 Esto equivale a considerar fracciones como: un medio, un tercio, un cuarto, etc., de ahí que las sumas defracciones unitarias se conozcan como fracción egipcia. Se puede demostrar además, que cualquier número racional positivo se puede escribir como fracción egipcia. El jeroglífico de una boca abierta

Fracciones Equivalentes:

Dos o más fracciones son equivalentes cuando representan la misma cantidad, y se escriben distinto.

Dos fracciones son equivalentes si pueden obtenerse una a partir de la otra, multiplicando (o dividiendo) por uno.

El conjunto de todas las fracciones equivalentes a una fracción dada, se llama número racional, y suele representarse por la única fracción equivalente irreducible del conjunto.

Los métodos de sumas y restas de fracciones con distintos denominadores se basa en llevar las fracciones 

a fracciones equivalentes con igual denominador. Los distintos procedimientos se sintetizan en 

procedimiento aplicados de una manera mecánica. En esta página no sólo queremos mostrarte los distintos 

procedimientos, sino la justificación de los mismos con ejemplos ilustrativos de distintas situaciones

Suma y resta con iguales denominadores:

Las fracciones constan de dos números. El número superior es llamado numerador. El número inferior es llamado denominador.

      -numerador  

    -denominador

Para sumar dos fracciones con el mismo denominador, suma los numeradores y coloca el resultado sobre el denominador común.

Suma y resta con distintos denominadores:

Cómo sumar fracciones con diferentes denominadores:

• Encuentra el mínimo común múltiplo (MCM) de las fracciones
• Renombra las fracciones para obtener el MCM
• Suma los numeradores de las fracciones                                   
• Simplifica la fracción

División de fracciones:

Para dividir fracciones por números naturales:

• Considera el entero como una fracción (es decir colócalo sobre el denominador 1).
• Invierte (es decir da vuelta) la segunda fracción y multiplica las fracciones.
• Multiplica los numeradores de las fracciones
• Multiplica los denominadores de las fracciones
• Coloca el producto de los numeradores sobre el producto de los denominadores.
• Simplifica la fracción

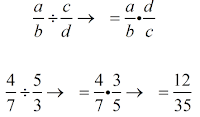
Multiplicación de fracciones:

Para multiplicar fracciones:

• Multiplica los numeradores de las fracciones
• Multiplica los denominadores de las fracciones
• Coloca el producto de los numeradores sobre el producto de los denominadores
• Simplifica la fracción

Criterios de divisibilidad:

los principales son:

• Los números son divisibles por 2 si las unidades son exactamente divisibles por 2. Esto significa que los números pares se pueden dividir por dos.

• Los números son divisibles por 3 si la suma de los dígitos es exactamente divisible por 3. Por ejemplo, la suma de los dígitos del número 3627 es 18, que es divisible por 3, entonces el número 3627 es divisible por 3.

• Los números son exactamente divisibles por 5 si el último dígito del número es 0 o 5.

bibliografia:

wikipedia, 2013, fracciones, (http://es.wikipedia.org/wiki/Fracci%C3%B3n), 25-10-2013

banfill . A, 2006, fracciones- tabla de contenidos, (http://www.aaamatematicas.com/fra.htm), 25-10-2013